재귀함수
자기 자신을 다시 호출하는 함수를 말한다.
같은 행위를 반복하는 경우 재귀함수를 사용하면 훨씬 코드가 간결해진다.
예시: factorial(팩토리얼), 피보나치수열, 하노이의 탑, 유클리드 호제법
def recursive_test():
print("Hello World")
recursive_test()
recursive_test()
재귀함수의 종료조건을 넣지 않으면?
만약 재귀함수의 종료 조건을 넣지 않으면 함수를 무한히 호출한다. 따라서 아래와 같은 에러 문구를 만나게 된다. 이유는 보통 인터프리터는 호출횟수 제한이 있는데 이 한계를 벗어났기 때문이다.
RecursionError: maximum recursion depth exceeded while calling a Python object
예시 1 - factorial 구현
팩토리얼은 1부터 시작하여 어떤 범위에 있는 모든 정수의 곱을 말한다.(ex) 5!=5x4x3x2x1=120) 팩토리얼을 재귀함수를 사용하여 구현하면 아래와 같다.
def factorial(n):
if n <= 1:
return 1
return n * recursive_factorial(n - 1)
print(recursive_factorial(5)) ##결과는 120계산 과정 및 순서는 아래와 같다.

예시 2 - 피보나치 수열
피보나치 수열은 첫 번째 항의 값이 0이고 두 번째 항의 값이 1일 때, 이후에 이어지는 항은 이전의 두 항을 더한 값으로 이루어지는 수열을 말한다. (1,1,2,3,5,8,13,21....) 피보나치 수열을 재귀함수를 사용하여 구현하면 아래와같다.
def fibo(n):
if n == 1 or n == 2:
return 1
else:
return fibo(n-1) + fibo(n-2)
print(fibo(6)) ## 결과는 8계산 과정 및 순서는 아래와 같다.

예시 3 - 하노이의 탑
하노이의 탑은 서로 크기가 다른 원반이 n개 있고 원반을 옮기는 3개의 기둥이 있는데, 어떻게 하면 원반 n개를 맨 왼쪽 기둥에서 맨 오른쪽 기둥으로 모두 옮기는 게임이다.

여기에는 세부 규칙이 있다.
1. 원반은 한 번에 한 개씩만 옮길 수 있다.
2. 원반을 뽑을 땐 기둥의 맨 위의 원반을 뽑아야 한다. (중간에 있는 원반은 어떤 경우에도 뽑을 수 없다.)
3. 원반을 쌓을 땐 기둥의 맨 위에 쌓아야 한다. (원반과 원반 사이에 끼워 넣을 수 없다.)
4. 원반을 쌓을 땐 큰 원반 위에 작은 원반을 올려야 한다. (작은 원반 위에 큰 원반을 올릴 수 없다.)
이 규칙을 지키면서 원반을 옮겨야 한다.
def hanoitop(n, start, destination, temp):
## 원반이 1개일 때 시작 기둥에서 도착 기둥까지 한 번에 이동
if n <= 1:
print("{0}번 원반을 {1}에서 {2}로 이동".format(n, start, destination))
return 1
count = 0
count += hanoitop(n - 1, start, temp, destination) ## 원반 n-1개를 시작 기둥에서 보조 기둥으로 이동
print("{0}번 원반을 {1}에서 {2}로 이동".format(n, start, destination))## 가장 큰 원반을 시작 기둥에서 도착 기둥으로 이동
count += 1
count += hanoitop(n - 1, temp, destination, start) # 원반 n-1개를 보조 기둥에서 도착 기둥으로 이동
return count
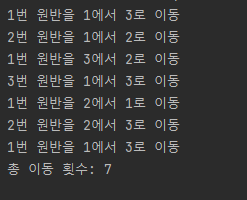
total_count = hanoitop(3, 1, 3, 2)
print('총 이동 횟수:', total_count)원반이 N개 있을 때 아래와 같은 로직을 이용하여 구현한다.
1. A 기둥에 있는 n-1 개의 원반을 B 기둥으로 옮깁니다. (재귀함수 사용)
2. A 기둥에 남아 있는 원반중 가장 큰 원반을 C 기둥으로 옯깁니다.
3. B 기둥에 있는 n-1개 원반을 C 기둥으로 옮깁니다. (재귀함수 사용)
예시 4 - 유클리드 호제법을 이용한 최대공약수 구하기
두 개의 자연수에 대한 최대공약수를 구하기 위해 유클ㄹ드 호제법을 이용하여 구할 수 있다. 유클리드 호제법은 아래의 조건을 따른다.
1. 두 자연수 A, B에 대하여 (A > B) A를 B로 나눈 나머지를 R이라고 하자
2. 이때 A와 B의 최대공약수는 B와 R의 최대공약수와 같다
def gcb(a,b):
if a%b==0:
return b
else:
return gcb(b,a%b)
print(gcb(12,8)) ## 결과는 4조건 1,2를 지키면서 재귀함수를 구현하면 아래와 같은 순서로 된다.
| 단계 | A | B |
| 1 | 12 | 8 |
| 2 | 8 | 4 |
따라서 최대공약수를 구하면 4가 나온다.
'Programming > 알고리즘 & 자료구조' 카테고리의 다른 글
| [알고리즘][이코테] Greedy Algorithm(그리디 알고리즘) (2) | 2022.03.10 |
|---|---|
| [알고리즘][이코테] Complexity(복잡도)와 Big-O 표기법 (2) | 2022.03.09 |
| [자료구조] Graph(그래프) (0) | 2022.03.08 |
| [자료구조] Complete Binary Tree(완전이진트리) 와 Heap(힙) (0) | 2022.03.07 |
| [자료구조] Binary Search Tree(이진탐색트리,BST) (0) | 2022.03.07 |