완전 이진 트리
이진트리 중 노드 왼쪽부터 차례대로 채워져 있는 트리를 말한다.
무조건 왼쪽부터 데이터를 채우기 때문에 데이터를어떻게 넣는지에 관계없이 동일한 구조를 가진다.
배열을 사용한 코드 구현이 가능해진다. 코드가 짧아지고, 가독성도 좋아진다.

왼쪽 자식의 Index = 부모 노드의 index * 2
오른쪽 자식의 Index = 부모 노드의 index * 2+1
힙
완전 이진트리이고, 자식 노드들이 특정한 성질을 가지고 정렬되어 있는 구조
최소힙: 부모노드가 항상 자식 노드보다 작은 완전이진트리 형태(부모노드<자식노드)
최대힙: 부모 노드가 항상 자식노드보다 큰 완전 이진트리 형태(부모노드>자식노드)
우선수위 큐에 사용된다.
※ 최소힙을 구현에 대해 공부할 예정입니다.
힙의 데이터 삽입 과정
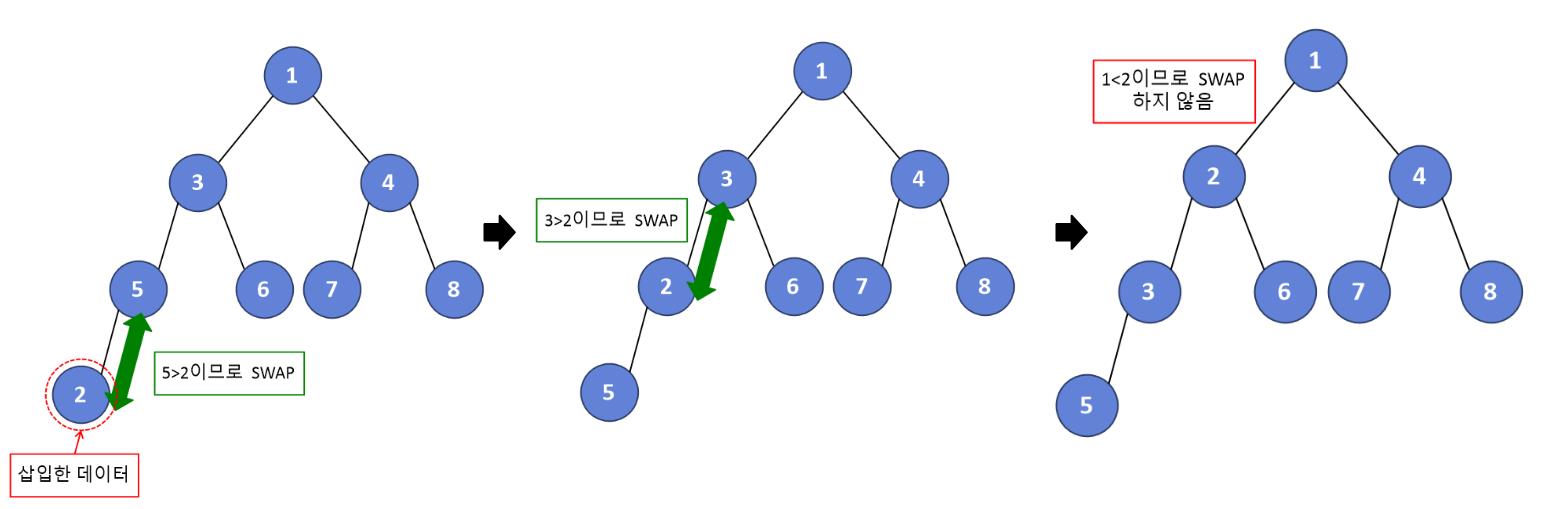
1. 새로운 데이터를 힙의 마지막 노드에 이어서 삽입한다.
2. 새로운 노드와 부모 노드를 비교한다. 새로운 노드가 더 작을 경우 부모와 새로운 노드의 위치를 변경한다.
3. 2번 과정을 위치 변경이 더이상 일어나지 않을 때까지 반복한다.
힙의 데이터 추출 과정
힙에서는 항상 루트노드의 데이터를 추출한다.

1. 루트 노드를 추출한다.
2. 마지막 노드를 루트 노드 위치로 이동시킨다.
3. 변경된 루트 노드와 두 자식 노드 중 더 작은 값을 가지는 노드의 위치와 변경한다.
4. 더이상 위치가 변경되지 않을 때까지 반복한다.
힙 구현하기
MAX_HEAP_SIZE = 101
class Heap:
def __init__(self):
self.arr = [None] * MAX_HEAP_SIZE
self.heap_count = 0힙을 사용할 때는 완전 이진트리 구조이므로 배열을 사용해 구현한다.
힙의 데이터 삽입 구현하기
MAX_HEAP_SIZE = 101
class Heap:
def __init__(self):
self.heap = [None] * MAX_HEAP_SIZE
self.heap_count = 0
def compare_with_parent(self, index):
if index <= 1:
return False
parent_index = index // 2 ## 부모 Node 계산
if self.heap[index] < self.heap[parent_index]: ## 부모 Node 값>자식 Node 값이면 SWAP
return True
else:
return False
## Heap에 Data 삽입하기
def insert(self, data):
self.heap_count += 1
if self.heap_count == 1: ## Root Node일 경우
self.heap[self.heap_count] = data
return
self.heap[self.heap_count] = data
insert_index = self.heap_count
while self.compare_with_parent(insert_index): ## 부모 Node 값과 자식 Node 값 비교
parent = insert_index // 2
## 부모 node 값>자식 node 값 이면 두 값을 변경
val=self.heap[insert_index]
self.heap[insert_index]=self.heap[parent]
self.heap[parent]=val
insert_index = parent ## 변경한 Node를 다시 비교함
return True
heap = Heap()
heap.insert(1)
heap.insert(3)
heap.insert(4)
heap.insert(5)
heap.insert(6)
heap.insert(7)
heap.insert(8)
heap.insert(9)
heap.insert(10)
heap.insert(11)
heap.insert(2)Heap의 삽입 과정 구현은 아래와 같다.
1. 가장 마지막 heap의 위치에 Data를 삽입한다.
2. 새로 삽입합 노드의 Data와 부모 노드를 비교한다. 새로운 노드의 Data가 더 작을 경우 부모와 Data의 위치를 바꾼다.
3. 2번을 계속 반복하여 더이상 위치 변경이 일어나지 않을 때 까지 반복한다.
힙의 데이터 추출 구현하기(중복 내용은 생략)
MAX_HEAP_SIZE = 101
class Heap:
def __init__(self):
self.heap = [None] * MAX_HEAP_SIZE
self.heap_count = 0
def compare_with_parent(self, index):
....
## Heap에 Data 삽입하기
def insert(self, data):
....
def compare_with_child(self, index):
left = 2 * index
right = 2 * index + 1
## 현재 Heap의 왼쪽과 오른쪽에 연결된 node가 없는 경우
if self.heap[left] == None and self.heap[right] == None:
return False
## heap의 왼쪽에 연결된 Node가 있는 경우
if self.heap[right] == None:
if self.heap[left] < self.heap[index]: ## 현재 Node 값>왼쪽 Node의 값이면
return left
else:
return False
## heap의 왼쪽가 오른쪽에 연결된 Node가 있는 경우
if self.heap[left] < self.heap[right]: ## heap의 왼쪽 값<오른쪽 값이면
return left
else:
return right
def pop(self):
index = 1
root = self.heap[1] ## Root의 값을 추출한다.
## 맨 마지막 Heap data를 Root로 옮긴다.
terminal_data = self.heap[self.heap_count]
self.heap[self.heap_count] = None
self.heap[index] = terminal_data
self.heap_count -= 1
while True:
child_index = self.compare_with_child(index)
if not child_index:
break
## child node 값<현재 node 값 이면 두 값을 변경
val = self.heap[child_index]
self.heap[child_index] = self.heap[index]
self.heap[index]= val
index = child_index
return root
heap = Heap()
heap.insert(1)
heap.insert(3)
heap.insert(4)
heap.insert(5)
heap.insert(6)
heap.insert(7)
heap.insert(8)
heap.insert(9)
heap.insert(10)
heap.insert(11)
heap.insert(2)
print(heap.heap)
heap.pop()
print(heap.heap)Heap의 추출 과정 구현은 아래와 같다.
1. 루트 노드를 추출한다. 그리고 마지막 노드를 루트 노드 위치로 이동시킨다.
2. 변경된 루트 노드와 두 자식 노드 중 더 작은 값을 가지는 노드의 위치와 변경한다.
3. 더이상 위치가 변경되지 않을 때까지 반복한다.
'Programming > 알고리즘 & 자료구조' 카테고리의 다른 글
| [알고리즘] recursive function(재귀함수) (0) | 2022.03.08 |
|---|---|
| [자료구조] Graph(그래프) (0) | 2022.03.08 |
| [자료구조] Binary Search Tree(이진탐색트리,BST) (2) | 2022.03.07 |
| [자료구조] Tree(트리) (0) | 2022.03.06 |
| [자료구조] Linked List(링크드 리스트) (0) | 2022.03.05 |