정리 내용은 [2022 ADsP 데이터 분석 준전문가]책을 기반으로 작성하였습니다.
2022 ADsP 데이터 분석 준전문가 - 교보문고
본 도서는 한국데이터베이스진흥원에서 실시하고 있는 『데이터 분석 전문가(ADP)』 자격증과 『데이터 분석 준전문가(ADsP)』 자격증을 준비하는 수험생들을 위한 도서이다. 2014년 4월 이후 시행
www.kyobobook.co.kr
1. 데이터 마이닝의 개요
1. 데이터 마이닝
데이터 마이닝은 대용량 데이터에서 의미 있는 패턴을 파악하거나 예측하여 의사결정에 활용하는 방법
데이터 마이닝과 통계분석과 차이점
통계분석: 가설이나 가정에 따른 분석이나 검증
데이터 마이닝: 다양한 수리 알고리즘을 통해 데이터베이스의 데이터로부터 의미 있는 정보를 찾아내는 방법
데이터 마이닝 종류
정보를 찾는 방법론에 따른 종류: 인공지능, 의사결정나무, K-평균군집화, 연관분석, 회귀분석, 로짓분석, 최근접이웃
분석 분석대상, 활용 목적, 표현방법에 따른 분류: 시각화 분석, 분류, 군집화, 포케스팅
데이터 마이닝 사용분야
병원에서 환자 데이터를 이용해서 해당 환자에게 발생 가능성이 높은 병을 예측
기존 환자가 응급실에 왔을 때 어떤 조치를 먼저 해야 하는지 결정
고객 데이터를 이용해 해당 고객의 우량/불량을 예측해 대출 적격 여부 판단
세관 검사에서 입국자의 이력과 데이터를 이용해 관세 물품 반입 여부 예측
데이터 마이닝 최근 환경
데이터 마이닝 도구가 다양하고 체계화되어 환경에 적합한 제품을 선택하여 활용 가능하다.
알고리즘에 대한 깊은 이해가 없어도 분석에 큰 어려움이 없다.
분석 결과의 품질은 분석가의 경험과 역량에 따라 차이가 나기 때문에 분석 과제의 복잡성이나 중요도가 높으면 풍부한 경험을 가진 전문가에게 의뢰할 필요가 있다
국내에서 데이터 마이닝이 적용된 시기는 1990년대 중반이다.
2000년대에 비즈니스 관점에서 데이터 마이닝이 CRM의 중요한 요소로 부각되었다.대중화를 위해 많은 시도가 있었으나 통계학 전문가는 대기업 위주로 진행되었다.
2. 데이터 마이닝 분석방법
| 분석방법 | 내용 |
| 지도학습 | 의사결정나무, 인공신경망, 일반화 선형 모형, 회귀분석, 로지스틱 회귀분석, 사례기반 추론, 최근접 이웃법 |
| 비지도학습 | OLAP, 연관성 규칙발견, 군집분석, SOM |
3. 분석 목적에 따른 작업유형 기법
| 목적 | 작업유형 | 설명/사용기법 |
| 예측 | 분류규칙 Classfication |
가장 많이 사용되는 작업. 과거의 데이터로부터 고객특성을 찾아내어 분류모형을 만들어 이를 토대로 새로운 레코드의 결과값을 측하는 것으로 목표 마케팅 및 고객 신용평가 모형에 활용 회귀분석, 판별분석, 신경망, 의사결정 나무 |
| 설명 | 연관규칙 Association |
데이터 안에 존재하는 항목간의 종속관계를 찾아내는 작업. 제품이나 서비스의 교차판매, 매장진열, 첨부우편, 사기적발 등의 다양한 분야에 활용됨 동시발생 매트릭스 |
| 연속규칙 Sequence |
연관규칙이 시간관련 정보가 포함된 형태. 고객의 구매이력속성이 반드시 필요하며 목표마케팅이나 일대일마케팅에 활용 동시발생 매트릭스 |
|
| 데이터군집화 Clustering |
고객레코드들을 유사한 특성을 지닌 몇개의 소그룹으로 분할하는 작업. 작업의 특성이 분류 규칙과 유사하나 분석대상 데이터에 결과값이 없으며 판촉활동이나 이벤트 대상을 선정하는데 활용 K-Means Clustering |
4. 데이터 마이닝 추진단계
[1단계] 목적 설정
데이터 마이닝을 통해 무엇을 왜 하는지 명확한 목적을 설정. 전문가가 참여해 목적에 따라 사용할 모델과 필요할 데이터를 정의
[2단계] 데이터 준비
고객정보, 거래정보, 상품정보, 마스터 정보, 웹로그 데이터, 소셜 네트워크 데이터 등 다양한 데이터를 활용
IT부서와 사전에 협의하고 일정을 조율하여 데이터 접근 부하에 유의하여야 하며, 필요시 다른 서버에 저장하여 운영에 지장이 없도록 데이터 준비
데이터 정재를 통해 데이터 품질을 보장하고, 필요시 데이터 보강하여 충분한 데이터를 확보
[3단계] 가공
모델링 목적에 따라 목적 변수 정의. 필요한 데이터를 데이터 마이닝 소프트웨어에 적용할 수 있는 형식으로 가공
[4단계] 기법 적용
1단계에서 명확한 목적에 맞게 데이터 마이닝 기법을 적용하여 정보 추출
[5단계] 검증
데이터 마이닝으로 추출된 정보를 검증. 테스트 데이터와 과거 데이터를 활용하여 최적의 모델 선정
검증이 완료되면 IT 부서와 협의해 상시 데이터마이닝 결과를 업무에 적용하고 보고서를 작성하여 추가 수익과 투자 대비 성과(ROI)등으로 기대효과를 전파
5. 데이터 마이닝을 위한 데이터 분할
모델 평가용 테스트 데이터와 구축용 데이터로 분할하여 구축용 데이터로 모형을 생성하고 테스트 데이터로 모형이 얼마나 적합한지 판단
데이터 분할
구축용(50%): 추정용, 훈련용 데이터라고도 불리며 데이터 마이닝 모델을 만드는데 활용
검정용(30%): 구축된 모형의 과대추정 또는 과소추정을 미세 조정하는데 활용
시험용(20%): 테스트 데이터나 과거 데이터를 활용하여 모델의 성능을 검증하는데 활용
데이터 양이 충분하지 않거나 입력 변수에 대한 설명이 충분한 경우
1) 홀드 아웃 방법: 주어진 데이터를 랜덤 하게 두 개의 데이터를 주어진 데이터를 랜덤 하게 두 개의 데이터로 구분하여 사용하는 방법. 주로 학습용과 시험용으로 분리하여 사용
2) 교차 확인방법: 주어진 데이터를 k개의 하부 집단으로 구분하여 k-1개의 집단을 학습용으로 나머지 하부 집단으로 검증용으로 설정하여 학습한다. k번 반복 측정한 결과를 평균 낸 값을 최종 값으로 사용. 주로 10-fold 교착 분석을 많이 사용
6. 성과분석

정분류율(Accuracy,AR)=(TN+TP)/(TN+TP+FN+FP)
오분류율(Error Rate)= 1-Accuracy =(FN+FP)/(TN+TP+FN+FP)
민감도(Sensitivity, TPR)=TP/(TP+FN) # True인 케이스에서 True로 예측한 비율
특이도(Specificity,TNR)=TN/(TN+FP)FPR=1-Specificity # False인 케이스에서 True로 예측한 비율
정확도(Precision)=TP/(TP+FP)
재현율(Recall)=TP/(TP+FN)
F1 Score(F₁)=(Precision * Recall)/(Precision + Recall)
* 정확도는 높을수록 좋다. 하지만 모두 부정일 경우 AR이 높아도 의미가 없다. 이것을 민감도(True가 True로 판정하는 정보)와 특이도(False가 False로 판정하는 정보)로 보완할 수 있다.
ROC Curve(Receiver Operating Characteristic Curve)
가로축을 FPR(False, positive Rate, 1-특이도) 값으로 두고 세로축을 TPR(True Positive Rate, 민감도) 값을 두어 시각화 한 그래프
2진 분류에서 모형의 성능을 평가하기 위해 많이 사용되는 척도
그래프가 왼쪽 상단에 가깝게 그려질수록 올바르게 예측한 비율은 높고, 잘못 예측한 비율이 낮음
따라서 AUROC(Area Under ROC, ROC곡선 아래의 면적)가 값이 클수록 성능이 좋음
TPR(True Positive Rate, 민감도): 1인 케이스 대한 1로 예측한 비율
FPR(False, positive Rate, 1-특이도): 0인 케이스에서 1로 잘못 예측한 비율
AUROC를 이용한 정확도 판단 기준: 0.9~1(excellent) / 0.8~0.9(good) / 0.7~0.8(fair) / 0.6~0.7(poor) / 0.5~0.6(fail)

이익도표
분류 모형의 성능을 평가하기 위한 척도로, 분류된 관측치에 대해 얼마나 예측이 잘 이루어졌는지 나타내기 위해 임의로 나눈 각 등급별로 반응 검출율, 반응률, 리프트 등의 정보를 산출하여 나타내는 도표
이익 도표의 각 등급은 예측 확률에 따라 매겨진 순위이기 때문에 상위등급에서는 더 높은 반응률을 보이는 것이 좋은 모형이라고 평가할 수 있다.
등급별 향상도가 급격하게 변동할수록 좋은 모형이라고 할 수 있고, 각 등급별로 향상도가 들쭉날쭉하면 좋은 모형이라고 볼 수 없다.
Lift(향상도)= 반응률/기본 향상도 * 좋은 모델이면 Lift가 빠른 속도로 감소해야 한다
과적합-과대 적합, 과소 적합
과적합-과대적합(Overfitting): 모형이 학습용 데이터를 과하게 학습하여 학습 데이터에 대해서는 높은 정확도를 나타내지만 테스트 데이터 혹은 다른 데이터에 적용할 때는 성능이 떨어지는 현상
과소 적합(Underfitting): 모형이 너무 단순하여 데이터 속 내재되어 있는 패턴이나 규칙을 제대로 학습하지 못하는 경우
2. 분류 분석
1. 분류 분석과 예측
| 분류분석 | 예측분석 | |
| 정의 | 데이터가 어떤 그룹에 속하는지 예측하는데 사용하는 기법. 클러스터링과 유사하지만 분류분석은 각 그룹이 정의되어 있음. 교사학습에 해당하는 예측기법 | 시계열분석처럼 시간에 따른 값 두 개만을 이용해 앞으로의 매출 또는 온도 등을 예측. 모델링을 하는 입력데이터가 어떤 것인지에 따라 특성이 다름. 여러 개의 다양한 설명변수(독립변수)가 아닌 한 개의 설명변수로 생각하면 된다. |
| 공통점 | 레코드의 특정 속성의 값을 미리 알아맞힘 | |
| 차이점 | 레코드(튜플)의 범주형 속성 값을 알아맞힘 | 레코드(튜플)의 연속형 속성 값을 알아맞힘 |
| 예 | 학생들의 국,영,수 점수를 통해 내신을 맞힘 카드 회사에서 회원들의 가입 정보를 통해 1년후 신용등급을 알아맞힘 |
학생들의 여러 가지 정보를 입력하여 수능점수를 맞힘 카드회사 회원들의 가입정보를 통해 연 매출액을 맞힘 |
분류 모델링
신용평가모형, 사기 방지 모형, 이탈 모형, 고객 세분화
분류 기법
회귀분석, 로지스틱 회귀분석 / 의사결정나무, CART, C5.0 / 베이지안 분류, Naive Bayesian / 인공신경망 / 지지도벡터기계 / k 최근접이웃 / 규칙 기반의 분류와 사례기반 추론
2. 로지스틱 회귀 분석
반응 변수가 범주형인 경우에 적용되는 회귀분석모형
새로운 설명변수(예측 변수)가 주어질 때 반응 변수의 각 범주에 속할 확률이 얼마인지를 추정(예측모형)
추정 확률을 기준치에 따라 분류하는 목적(분류 모형)으로 활용된다.
이때 모형의 적합을 통해 추정된 확률을 사후 확률이라 함
설명변수가 한 개인 경우 해당 회귀 계수의 부호에 따라 S자 모양(S>0) 또는 역 S자 모양(S <0) 모양을 가진다.
표준 로지스틱 분포의 누적 함수 분포로 성공의 확률을 추정
glm() 함수 사용
로지스틱 회귀모형이 선호되는 이유
독립변수에 대해 어떤 가정도 필요하지 않음
독립변수가 연속형 및 이산형 모두 가능하기 때문에 판별분석보다 선호됨
오즈비(Odds Ratio)
오즈(odds): 성공할 확률이 실패할 확률의 몇 배인지를 나타내는 확률
오즈비(odds ratio) 오즈의 비율
성공 가능성이 높은 경우 1보다 크고 실패 가능성이 높은 경우 1보다 작다.
선형 회귀 분석 vs 로지스틱 회귀 분석
| 선형회귀분석 | 로지스틱 회귀분석 | |
| 종속변수 | 연속형 변수 | (0,1) |
| 계수 추정법 | 최소제곱법 | 최대우도 추정법 |
| 모형검정 | F-검정, T-검정 | 카이제곱 검정 |
| 그래프 |  |
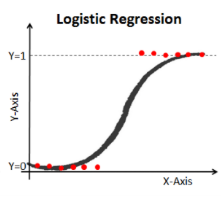 |
최대 우도 추정법(MLE)
모수의 미지의 θ인 확률분포에서 뽑은 표본(관측치) x들을 바탕으로 θ를 추정하는 기법
표본의 수가 클수록 최대 우도 추정법은 안정적
우도: 이미 주어진 표본 x들에 비추어봤을 때 모집단의 모수 θ에 대한 추정이 그럴듯한 정도를 말한다
우도 L(x|θ)은 θ가 전재되었을 때 표본 x가 등장할 확률인 P(x|θ)에 비례
카이제곱 검정
분류 조합에 따라 특정값에 유효한 차이가 발생하는 지를 검정하는 것으로 명목 척도로 측정된 두 속성이 서로 관련되어 있는지 분석하고 싶을 때 사용하는 통계 분석방법
독립변수와 종속변수가 모두 명목 척도일 경우 적합한 통계 기법
3. 의사결정 나무
의사결정 나무는 분류 함수를 의사결정 규칙으로 이뤄진 나무 모양으로 그리는 기법
나무 구조는 연속적으로 발생하는 의사결정 문제를 시각화해 의사결정이 이뤄지는 시점&성과를 한눈에 볼 수 있다.
계산 결과가 의사결정 나무에 직접 나타나기 때문에 해석이 간편하다.
의사결정나무는 주어진 입력값에 대하여 출력 값을 예측하는 모형으로 분류 나무와 회귀 나무 모형이 있다.
의사결정 나무 구성요소
뿌리마디: 시작되는 마디로 전체 자료 포함
자식마디: 하나의 마디로부터 분리되어 나간 2개 이상의 마디들
부모마디: 주어진 마디의 상위 마디
끝마디: 자식이 없는 마디
중간마디: 부모와 자식마디가 모두 있는 마디
가지: 뿌리 마디로부터 끝마디까지 연결된 마디들
깊이: 뿌리 마디부터 끝마디까지 중간 마디의 수
예측력과 해석력
기대 집단의 사람들 중 가장 많은 반응을 보일 때 고객 유치방안을 예측하고자 하는 경우 예측력에 치중한다.
신용평가에서 심사 결과 부적격 판정이 나온 경우 고객에게 부적격 이유를 설명해야 하므로 해석력에 치중한다.
의사결정 활용
세분화: 데이터를 비슷한 특성을 갖는 몇 개의 그룹으로 분할해 그룹별 특성을 발견
분류: 여러 예측 변수들에 근거해 관측 개체의 목표 변수 범주를 몇 개의 등급으로 분류하고자 하는 경우에 사용
예측: 자료에서 규칙을 찾아내고 이를 이용해 미래의 사건을 예측하고자 하는 경우
차원 축소 및 변수 선택: 매우 많은 수의 예측변수 중에서 목표 변수에 큰 영향을 미치는 변수들을 골라내고자 하는 경우에 사용
교호 작용효과의 파악: 여러 개의 예측 변수들을 결합해 목표 변수에 작용하는 규칙을 파악하고자 하는 경우 범주형 변수의 범주를 소수의 몇 개로 병합하거나 연속형 목표 변수를 몇 개의 등급으로 이산화 하고자 하는 경우
의사결정 나무의 특징 - 장점
결과를 누구에게나 설명하기 용이 모형을 만드는 방법이 계산적으로 복잡하지 않음
대용량의 데이터에서도 빠르게 만들 수 있음
비정상 잡은 데이터에 대해서도 민감함이 없고 분류할 수 있음
한 변수와 상관성이 높은 다른 불필요한 변수가 있어도 크게 영향을 받지 않음
설명변수나 목표 변수에 수치형 변수와 범주형 변수를 모두 사용 가능함
모형 분류 정확도가 높다
의사결정 나무의 특징 - 단점
새로운 자료에 대한 과대 적합이 발생할 가능성이 높다
분류 경계선 부군의 자료 값에 대해서 오차가 크다
설명변수 간의 중요도를 판단하기 쉽지 않다.
의사결정 나무 분석과정
1) 성장단계: 각 마디에서 적절한 최적의 분리 규칙을 찾아 나무를 성장시키는 과정 적절한 정지 규칙을 만족하면 중단
2) 가지치기 단계: 오차를 크게 할 위험이 높거나 부적절한 추론 규칙을 가지고 있는 가지 또는 불필요한 가지 제거
3) 타당성 및 평가 단계: 이익도표, 우험도표, 혹은 시험자료를 이용하여 의사결정나무를 평가
4) 해석 및 예측 단계: 구축된 나무모형 해석하고 예측 모형을 설정한 후 예측에 적용
나무의 성장
나무모형의 성장과정은 x들로 이루어진 입력 공간을 재귀적으로 분할하는 과정
1) 분리 규칙
분리 변수가 연속형: A=x≤s / 분리 변수 범주형 {1, 2, 3, 4}: A=1,2,4 와 A의 여집합=3으로 나뉨
최적 분할의 결정은 불순도 감소량을 가장 크게 하는 분할
각 단계에서 최적 분리기준에 의한 분할을 찾은 다음 각 분할에 대하여도 동일한 과정 반복
2) 분리기준
| 목표변수 | 기준값 | 분리기준 |
| 이산형 | 카이제곱 통계량 p값 | P값이 가장 작은 예측변수와 그때의 최적분리에 의해서 자식 마디 형성 |
| 지니지수 | 지니 지수를 감소시켜주는 예측변수와 그 때의 최적분리에 의해서 자식마디 선택 | |
| 엔트로피지수 | 엔트로피 지수가 가장 작은 예측변수와 이 때의 최적분리에 의해 자식마디를 형성 | |
| 연속형 | 분산분석에서 F 통계량 | P값이 가장 작은 예측변수와 그때의 최적분리에 의해서 자식 마디 형성 |
| 분산의 감소량 | 분산의 감소량을 최대화하는 기준의 최적분리에의해서 자식 마디 형성 |
3) 정지 규칙
더 이상 분리가 잃어 나지 않고, 현재의 마디가 끝마디가 되도록 하는 규칙
정지 기준: 의사결정 나무의 깊이를 지정, 끝마디의 레코드 수의 최소 개수를 지정
나무의 가지치기
너무 큰 나무모형은 자료를 과대 적합하고 너무 작은 나무모형은 과소 적합할 위험이 있다.
나무의 크기를 모형의 복잡도로 볼 수 있으며 최적의 나무 크기는 자료로부터 추정하게 된다.
일반적으로 사용되는 방법은 마디에 속하는 자료가 일정수(가령 5) 이하 때, 분할을 정지하고 비용-복잡도 가지치기를 이용하여 성장시킨 나무를 가지치기하게 된다.
4. 불순도의 여러 가지 측도
목표 변수가 범주형 변수인 의사결정 나무의 분류 규칙을 선택하기 위해서는 카이제곱 통제량, 지니 지수, 엔트로피 지수를 활용한다.
카이제곱 통계량
각 셀에 대한 ((실제도수-기대도수)의 제곱/기대도수)의 합으로 구할 수 있다.
기대도수=열의 합계 * 합의 합계 / 전체 합계

지니지수
노드의 불순도를 나타내는 방법. 지니지수의 값이 클수록 이질적, 순수도가 낮음

엔드로피 치수
열역학에 쓰는 개념으로 무질서 정도에 대한 측도. 엔트로피 지수의 값이 클수록 순수도가 낮음. 엔트로피 지수가 가장 낮은 예측변수와 이때의 최적분리 규칙에 의해 자식마디 형성

5. 의사결정 나무 알고리즘
CART(Classfication and regression Tree)
앞에서 설명한 방식의 가장 많이 활용되는 의사결정나무 알고리즘
불순도의 측도로 출력 변수가 범주형일 경우 지니지수를 이용, 연속형인 경우 분산을 이용한 이진분리를 사용개별 입력변수 뿐만 아니라 입력변수들의 선형결합들 중 최적의 분리를 찾을 수 있다.
C4.0와 C5.0
CART와 다르게 각 마디에서 다지분리가 가능하면 범주형 입력변수에 대해서는 범주의 수만큼 분리가 일어남
분순도의 측도로는 엔트로피 지수 사용
CHAID(CHi-squared Automatic Intergraction Detection)
가지치기를 하지 않고 적당한 크기에서 나무모형의 성장을 중지하고 입력변수가 반드시 범주형변수이어야 함
불순도의 측도로는 카이제곱 통계량 사용
3. 앙상블분석
1. 앙상블
앙상블 정의
주어진 자료로부터 여러 개의 예측모형들을 조합하여 하나의 최종 예측 모형을 만드는 방법. 다중 모델 조합, 분류기 조합이 있다.
학습방법의 불안전성
학습자료의 작은 변화에 의해 예측모형이 크게 변하는 경우 그 학습 방법은 불안정이다
가장 안정적인 방법으로는 1-near neighbor(가장 가까운 자료만 변하지 않으면 예측 모형이 변하지 않음), 선형회귀모형(최소제고법으로 추정해 모형 결정)이 존재한다
가장 불안정한 방법으로는 의사결정나무가 있다.
2. 앙상블 기법의 종류
배깅
주어진 자료에 여러개의 붓스트랩 자료를 생성하고 각 붓스트램 자료에 예측모형을 만든 후 결합하여 최종 예측모형을 만드는 방법
붓스트랩: 주어진 자료에서 동일한 크기의 표본을 랜덤 복원추출로 뽑은 자료를 의미
보팅: 여러 개의 모형으로부터 산출된 결과를 다수결에 의해서 최종결과를 선정하는 과정
최적의 의사결정나무를 구축할 때 가장 어려운 부분이 가지치기이지만 배깅에서는 가지치기 하지 않고 최대로 성장한 의사결정나무를 활용
훈련자료의 모집단의 분포를 모르기 때문에 실제 문제에서는 평균 예측 모형을 구할 수 없다
배깅은 이러한 문제를 해결하기 위해 훈련자료를 모집단으로 생각하고 평균예측모형을 구하여 분산을 줄이고 예측력을 향상시킬 수 있다.
부스팅
예측력이 약한 모형들을 결합하여 강한 예측모형을 만드는 방법
Adaboost: 부스팅 방법 중 하나. 이진분류 문제에서 랜덤분류기보다 조금 더 좋은 분류기 n개에 각각 가중치를 설정하고 n개의 분류기를 결합하여 최종 분류기를 만드는 방법(단, 가중치의 합은 1)
훈련오차가 빨리 그리고 쉽게 줄일 수 있다
배깅에 비해 많은 경우 예측오차가 향상 되어 Adaboost의 성능 배깅보다 뛰어난 경우가 많다.
랜덤 포레스트
의사결정나무의 특징인 분산이 크다는 점을 고려하여 배깅과 부스팅보다 더 많은 무작위성을 주어 약한 학습기들을 생성한 후 이를 선형결합하여 최종 학습기를 만드는 방법
randomForest 패키지는 random input에 따른 forest of free를 이용한 분류방법
랜덤한 forest에 많은 트리들이 생성됨
수천개의 변수를 통해 변수제거 없이 실행되므로 정확도 측면에서 좋은 성과를 보임
이론적설명이나 최종 결과에 대한 해석이 어렵다는 단점이 있지만 예측력이 매우 높다. 특히 입력변수가 많은 경우 배깅과 부스팅과 비슷하거나 좋은 예측력을 보인다
'Study > ADSP' 카테고리의 다른 글
| [ADsP] 최신 빅데이터 상식 (0) | 2022.03.11 |
|---|---|
| [ADsP] 3과목 데이터 분석 - 5장 정형 데이터 마이닝 (2) (0) | 2022.03.10 |
| [ADsP] 3과목 데이터 분석 - 4장 통계분석 (2) (0) | 2022.03.08 |
| [ADsP] 3과목 데이터 분석 - 4장 통계분석 (1) (0) | 2022.03.07 |
| [ADsP] 3과목 데이터 분석 - 3장 데이터마트 (0) | 2022.03.06 |